Question

I need help with number 5 pleaseeee I beg I will be so thankful:)

Answer 1

The answer to your problem is, 22.3 ft

Explanation:

Here we can make a triangle rectangle with the following vertex:

• The student's eye level.
• The top of the flagpole
• The intersection between a horizontal line that passes through her eye level and a point in the flagpole.

The catheti of this triangle rectangle will be:

• The distance between her and the flagpole (36ft)
• The height of the flagpole minus the height of her eye level = H
• We want to find the value of H.
• We also know that the angle of elevation from her point of view is 25°.

! Tan(a) = opposite cathetus/adjacent cathetus. !

Tan(25°) = H/36ft

Solving for H we ge; Tan(25°)*36ft = H = 16.8 ft

The height of the flag pole minus the height of her eye level, then the actual height of the flagpole is:

`H + 5.5ft = 16.8 ft + 5.5ft = 22.3 ft`

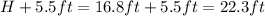
Thus the answer is, 22.3 ft