Question

You love to collect sports cards and started to keep track of your collection. After the first year you collected cards, you had 35 cards. After collecting for 3 years, you now have 103

sports cards.

If you collect the same number of cards each year, which point-slope equation could be used to predict how many cards you will have in any given year?

Answer 1

y - 35 = 34(x - 1)

y - 103 = 34(x - 3)

Explanation:

Let x be the number of years you collected sports cards.

Let y be the total number of sports cards collected.

From the given information, we can create two ordered pairs (x, y):

• (1, 35) and (3, 103).

If you collect the same number of cards each year, we can write a linear equation to predict how many cards you will have in any given year.

Determine the slope of the line by substituting the ordered pairs into the slope formula:

`\implies \textsf{Slope\:$(m)$}=\frac{\textsf{change\:in\:$y$}}{\textsf{change\:in\:$x$}}=(103-35)/(3-1)=(68)/(2)=34`

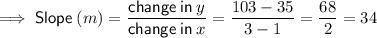
Therefore, the slope of the line is 34.

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Substitute the found slope m = 34 and point (1, 35) into the point-slope equation:

`y-35=34(x-1)`

Alternatively, substitute the found slope m = 34 and point (3, 103) into the point-slope equation:

`y-103=34(x-3)`

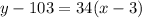
Therefore, the point-slope equations that could be used to predict how many cards you will have in any given year are:

• 
  `y-35=34(x-1)`

• 
  `y-103=34(x-3)`