Question

Calculate the potential energy, kinetic energy, mechanical energy, velocity, and height of the skater at the various locations

Answer 1

Equations/Concepts Used:

Kinetic Energy =>
`K=(1)/(2)mv^2`

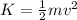
Gravitational Potential Energy =>
`U_(g)=mgy`

Mechanical Energy =>
`E_(Mech.)=U+K`

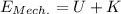
Conservation of Energy =>
`E_(0)=E_(f)`

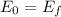
At point 1

`m=60 \ kg`

`v=8 \ m/s`

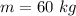
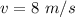
PE ==>
`U_(g)=mgy \Rightarrow =(60)(9.8)(0) \Rightarrow U_(g)= 0 \ J`

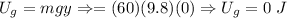
KE ==>
`K=(1)/(2)mv^2 \Rightarrow =(1)/(2)(60)(8)^2 \Rightarrow K=1920 \ J`

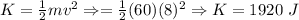
ME==>
`E_(Mech.)=U+K \Rightarrow = 0+1920 \Rightarrow E_(Mech.)=1920 \ J`

At point 2

`y=1 \ m`

Find the velocity of the skater at point 2 using conservation of energy.

We already found the total energy at point 1, which was 1920 Joules.

==>
`E_(1)=E_(2) \Rightarrow 1920=U_{g_(2)}+K_2 \Rightarrow 1920=(60)(9.8)(1)+(1)/(2)(60)v^2`

`\Rightarrow 1920=588+30v^2 \Rightarrow 1332=30v^2 \Rightarrow v^2=44.4 \Rightarrow v=6.66 \ m/s`

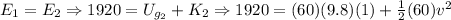
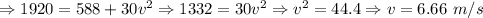
From the equation above we answered the following,

`v=6.66 \ m/s`

`U_g=588 \ J`

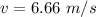
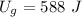
We know the velocity at point 2, find KE then ME.

`K=(1)/(2)(60)(6.66)^2 \Rightarrow K=1331 \ J`

`E_(Mech.)=588+1331 \Rightarrow E_(Mech.)= 1919 \ J`

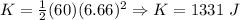
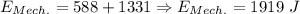
Notice how mechanical energy remains constant, this is because energy is a conserved quantity.

At point 3

Use conservation of energy again, using points 1 and 3.

==>
`E_1=E_3 \Rightarrow 1920=U_(g_3)+K_3 \Rightarrow 1920=(60)(9.8)h+0`

At point 3 the skaters velocity will go to 0 and all energy will be potential.

So,
`v=0 \ m/s`

`\Rightarrow 1920=588h \Rightarrow h=3.27 \ m`

==>
`U_g=(60)(9.8)(3.27) \Rightarrow U_g=1923 \ J`

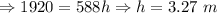
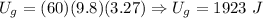
Answers:

Point 1, PE=0 J, KE=1920 J, ME=1920J

Point 2, PE=588 J, KE= 1331 J, ME= 1919 J, v=6.66 m/s

Point 3, PE=1923 J, KE=0 J ,ME= 1923 J, v=0 m/s, h=3.27 m