Question

PLEASE HELP!!

ABCD is a kite, so AC ⊥ DB and DE = EB. Calculate the length of AC, to the nearest tenth of a centimeter.

Answer 1

AC = 12.7 cm

Explanation:

To find:-

• The length of AC.

Answer :-

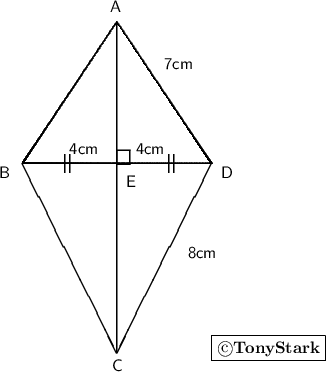
We are here given a kite in which AC ⊥ DB and DE = EB = 4cm . We are interested in finding out the length of AC .

`\rule{200}2`

D I A G R A M : -

`\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\qbezier(1, 0)(1,0)(3,3)\qbezier(5,0)(5,0)(3,3)\qbezier(5,0)(1,0)(1,0)\put(2.85,3.2){$\sf A$}\put(0.5,-0.3){$\sf B $}\put(5.2,-0.3){$\sf D $}\put(1,0){\line(1,-2){2}}\put(5,0){\line(-1, - 2){2}}\put(2.9,-4.4){$\sf C $}\put(3,3){\line(0, - 1){7}}\put(4,2){$\sf 7cm $}\put(4.5,- 2){$\sf 8cm $}\put(3.4,0.2){$\sf 4cm $}\put(2,.2){$\sf 4cm $}\put(3.2, - .5){$\sf E $}\multiput(2,0.2)(2.2,0){2}{\line(0,-1){0.4}}\multiput(1.9,0.2)(2.2,0){2}{\line(0,-1){0.4}}\put(5,-4){$\boxed{\bf \textcopyright Tony Stark}$}\put(3.01,0.01){\framebox(0.25,0.25)}\end{picture}`

`\rule{200}2`

We can see that,

`\sf:\implies AC = AE+EC\\`

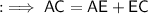
We can seperately find AE and EC and then add them up to find AC . We can see that due to the diagonals intersecting each other at right angles , there is formation of 4 right angled triangle, the triangles which we will be using are ∆AED and ∆CED .

We can use Pythagoras theorem here according to which

• The square of hypotenuse (longest side) is equal to the sum of squares of other two sides.

`\sf:\implies h^2 = a^2 + b^2 \\`

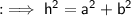
In two triangles AED and CED hypotenuse are 7cm and cm respectively.

So that , in ∆AED ,

`\sf:\implies 7^2 = AE^2 + DE^2 \\`

`\sf:\implies AE^2 = 7^2 - DE^2 = 7^2 - 4^2 \\`

`\sf:\implies AE^2 = 49 - 16 \\`

`\sf:\implies AE = √( 33) \\`

`\sf:\implies\red{ AE = 5.74} \\`

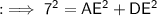
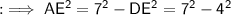
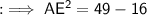
Similarly, in ∆CED ,

`\sf:\implies 8^2 = CE^2 + DE^2 \\`

`\sf:\implies CE^2 = 8^2 - DE^2 = 8^2 - 4^2 \\`

`\sf:\implies CE^2 = 64- 16 \\`

`\sf:\implies CE = √( 33) \\`

`\sf:\implies\red{ CE = 6.93} \\`

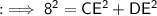
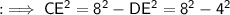
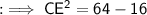
Now add them up to find AC , as ;

`\sf:\implies AC = AE + CE\\`

`\sf:\implies AC = 5.74 + 6.93 \\`

`\sf:\implies AC = 12.67 \\`

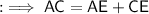
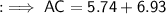
Rounding off to nearest tenth, will give us,

`\sf:\implies \red{ AC = 12.7 \ cm } \\`

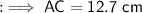
Hence the length of AC is 12.7 cm.

Answer 2

• 12.7 cm

----------------------------

Since diagonals of a kite are perpendicular to each other, the triangles AED and CED are right triangles.

Find the length of ED:

• ED = BE = BD/2 = 8 / 2 = 4 cm

Find the length of legs AE and CE using Pythagorean theorem:

• 
  `AE=√(AD^2-ED^2)=√(7^2-4^2)=√(49-16)=√(33)=5.74`
• 
  `CE=√(CD^2-ED^2)=√(8^2-4^2)=√(64-16)=√(48)=6.93`

Find the length of AC:

• AC = AE + CE = 5.74 + 6.93 = 12.67 ≈ 12.7 cm