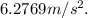Question

In the figure below, m₁ = 11.0 kg and m₂ = 4.5 kg. The coefficient of static friction between m, and the horizontal surface it

1711
M₂
(a) If the system is released from rest, what will its acceleration be?
m/s²
(b) If the system is set in motion with m₂ moving downward, what will be the acceleration of the system?
m/s²
17. [0/5 Points] DETAILS
PREVIOUS ANSWERS SERCP9 4.P.047.WI.
The coefficient of static friction between the m = 3.15-kg crate and the 35.00 in

Answer 1

See below.

Step-by-step explanation:

The list of given we have:

• 
  `m_1=11.0Kg`
• 
  `m_2=4.5Kg`
• 
  `u_s=0.60`
• 
  `u_k=0.30`

(a) We are asked to find the acceleration of the system if the system is released from rest.

We can simply distinguish between the forces operating on the two masses to provide an answer. We must first determine the force affecting the masses. Hence, the only force acting on mass 2 is the gravitational force since it is suspended from the cord.

`Fg=m_2g`

`F_g=(4.5Kg)(9.8m/s^2)`

`F_g=44.1N`

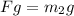
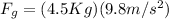
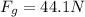
while for the mass 1 we have the static frictional force,

`f_s=u_sN`

`f_s=(0.60)(11.0Kg)(9.8m/s^2)`

`f_s=64.68N`

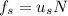
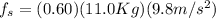
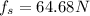
We may infer that if the system is released from rest, it does not move at all since the static frictional force acting on mass 1 was greater than the gravitational force acting on mass 2, which means the system's acceleration must be equal to
`a=0m/s^2`.

(b) We are asked to find the acceleration of the system if the mass 2 moves downward.

For this question, we must draw a free-body diagram (attachment #1).

Since we are able to draw a free-body diagram and identify the force(s) acting on the masses, we can find the acceleration of the system using the equation of Newton's second law, so we have:

`F_\text{net}=m_(sys) a`

`a=(F_(net))/(m_(sys))`

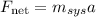
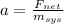
where the
`F_(net)` is the sum of force(s) acting on the system and
`m_(sys)` is the total mass of the system,

`a=(Fg_2-T+T-f_k)/(m_1+m_2)`

`a=(F_g2 - f_k)/(m_1+m_2)`

`a=(m_2g-u_km_1g)/(m_1+m_2)`

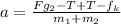
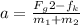
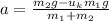
substituting all of the given

`a=((4.5Kg)(9.8m/s^2)-(0.30)(11.0Kg))/(11.0Kg-4.5Kg)`

`a=(40.8Kgm/s^2)/(6.5Kg)`

`a=6.2769`

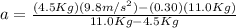
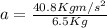
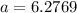
We can conclude that if the mass 2 is going downward then the acceleration of the system would be
`6.2769m/s^2.`