Question

What single percentage change is equivalent to a 17% decrease followed by a 12% increase?

2.96% decrease
7.04% increase
7.04% decrease

92.96% increase
2.96% increase
92.96% decrease

Answer 1

let's call our number hmmm Z, now, let's reduce it by 17%, so 100% - 17% = 83%, so the new size for Z is 83% off the original, hmm how much is that?

`\begin{array} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{83\% of Z}}{\left( \cfrac{83}{100} \right)Z}\implies 0.83Z`

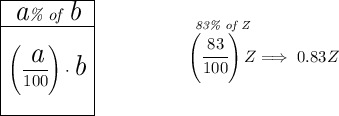
now, let's increase it by 12%, so the new size will be 100% + 12% = 112%, so 112% of 0.83Z, let's check how much is that

`\stackrel{\textit{112\% of 0.83Z}}{\left( \cfrac{112}{100} \right)0.83Z}\implies 0.9296Z`

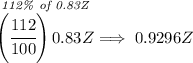
now, let's convert that to a percent format by simply multiplying it by 100, so that'd be 100 * 0.9296Z = 92.96% of Z. Well, hell 92.96% is less than 100%, so is really 100% - 92.96% = 7.04% less.

So, instead of all that rigamarole, we could have just reduced Z by 7.04% in one fell swoop and obtain the same thing.