Question

A bungee jumping company wants to set up a bungee

jumping location on the top of a bridge that is 300 m above
the ground. For safety reasons, the company wants to
select a bungee cord spring constant such that a jumper
with a mass of 115 kg will reach his lowest point that is,
the point when the change in gravitational potential energy
equals the amount of energy stored in the bungee cord at
the bottom of the jump - at 50 m above the ground. What
is the approximate spring constant the company should
choose, assuming that air resistance, friction, and the
weight of the cord can be ignored and that the cord
immediately begins to stretch as soon as the jumper
begins to fall? (Recall that g = 9.8 m/s²)
cord mg
A. 23 N/m
B. 9 N/m
C. 4 N/m
D. 15 N/m

Answer 1

Approximately
`9\; {\rm N \cdot m^(-1)}`.

Step-by-step explanation:

Change in the gravitational potential energy (GPE) of the system:

`(\text{change in GPE}) = m\, g\, \Delta h`, where:

• 
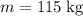  `m = 115\; {\rm kg}` is the mass of the jumper.
• 
  `g = 9.8\; {\rm m\cdot s^(-2)} = 9.8\; {\rm N\cdot kg^(-1)}` is the gravitational field strength.
• 
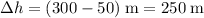  `\Delta h = (300 - 50)\; {\rm m} = 250\; {\rm m}` is the absolute value of the change in height.

Change in the elastic potential energy (EPE) of the system:

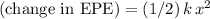`\text{(change in EPE)} = (1/2)\, k\, x^(2)`, where:

• 
  `k` is the spring constant and needs to be found.
• 
  `x = (250 - 0)\; {\rm m} = 250\; {\rm m}` is the change in the length of the cord. Note that since the cord started stretching immediately, that initial length of the cord would be
  `0\; {\rm m}` .

Set
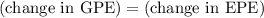`\text{(change in GPE)} = \text{(change in EPE)}` and solve for the spring constant
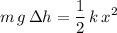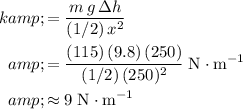`k`:

`\displaystyle m\, g\, \Delta h = (1)/(2)\, k\, x^(2)`.

`\begin{aligned}k &= (m\, g\, \Delta h)/((1/2)\, x^(2)) \\ &= ((115)\, (9.8)\, (250))/((1/2)\, (250)^(2))\; {\rm N\cdot m^(-1)} \\ &\approx 9\; {\rm N\cdot m^(-1)}\end{aligned}`.