Basic Proportionality Theorem (BPT): If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio. This is also known as Thales theorem.
Given:
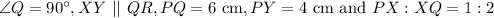
Since,
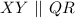 ,
,
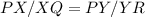
[ By Thales theorem (BPT)]

![[PX : XQ = 1 : 2]](https://img.qammunity.org/2024/formulas/mathematics/college/5l3u65lazd1kbmyhj2ajhbe4txyr2drlmb.png)

![[YR= PR - PY]](https://img.qammunity.org/2024/formulas/mathematics/college/mt1wi9ftiucivfyxkep6gw20mpaaxl5a22.png)
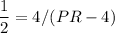


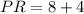
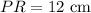
In right
 ,
,
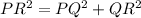
[ By Pythagoras theorem]

![[\text{Given} : PQ= 6 \ \text{cm}]](https://img.qammunity.org/2024/formulas/mathematics/college/ly55wc49vpk7dsjh4lxemt67c3axztzygd.png)
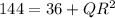
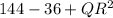
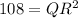
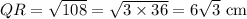
Hence, the lengths of PR and QR is 12 cm and
 cm.
cm.