Question

1-3x less than or equal to -2x< 3x+5​

Answer 1

x∈ [1; +∞)

Explanation:

First write down the whole inequality:

1 - 3x ≤ -2 ﹤ 3x + 5

Then it can be seen that there are two separate inequalities here, so we have a system of inequalities:

{1 - 3x ≤ -2,

{3x + 5 ﹥ -2;

we express x from both inequalities:

From the first one:

-3x ≤ -2 - 1

-3x ≤ -3 / : (-3)

x ≥ 1

From the second one:

3x ﹥ -2 - 5

3x ﹥ -7 / : 3

`x﹥ - (7)/(3)`

`x﹥ - 2 (1)/(3)`

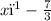
So, now that we have expressed x from both inequalities, we can write down the general range of x values for them (as you can see in the picture, the answer is the common values of x for both inequalities, both red and green colors):

x∈ [1; +∞)