Question

12+17+22+...+102

i will give brailiest to who answers first and is right

Answer 1

`a = 7`

`d = 12 - 7 = 5`

`L = 102`

`\implies a + (n-1)d = 102`

`\implies 7 + (n-1)(5) = 102`

`\implies (n-1)(5) = 95`

`\implies n - 1 = 19`

`\implies n = 20`

`\text{Required sum = n/2} \ (a + L)`

`= 20 /2 \ ( 7 + 102)`

`= 10 * 109`

`\bold{= 1090}`

Answer 2

The sum is 1090

Explanation:

S=7+12+17+22+...+102 ---> reason=5

We define the values, before starting:

Ratio = r , Term n = Tn , Term number = n , Term one = T1

To do this we first find the term number of 102, with the following formula:

Tn = t1 + (n - 1) r

102 = 7 + (n - 1) 5

102 = 7 + 5n - 5

102 = 5n + 2

100 = 5n

20 = n

Then we realize that 102 is the term N°20, now what we have to do is find the sum of the arithmetic series, with the following values and the following formula:

t1 = 7 , tn = 102 , n = 20

S = (
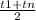`(t1+tn)/(2)`) . n

S = (
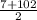`(7+102)/(2)`) . 20

S = 109 . 10

S = 1090