Question

In analyzing hits by certain bombs in a​ war, an area was partitioned into 561 ​regions, each with an area of 0.75 km2. A total of 525 bombs hit the combined area of 561 regions. Assume that we want to find the probability that a randomly selected region had exactly four hits. In applying the Poisson probability distribution​ formula, ​P(x)=

μx•e−μ
x!​, identify the values of μ​, ​x, and e. ​Also, briefly describe what each of those symbols represents.

Answer 1

x is the number of successes

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

There is a 17.18% probability that a randomly selected region had exactly two hits.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X=x)=(e^(-\mu)*\mu^x)/((x)!)`

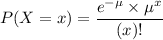
In which

x is the number of successes

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

In this problem we have that:

A total of 525 bombs hit the combined area of 561 regions. So the mean hits per region is:

`P=(525)/(561)=0.9358`

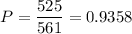
Assume that we want to find the probability that a randomly selected region had exactly two hits.

This is P(X = 2).

`P(X=x)=(e^(-\mu)*\mu^x)/((x)!)`

`P(X=2)=(e^(-0.9358)*(0.9358)^2)/((2)!)=0.1718`

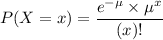
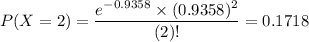
There is a 17.18% probability that a randomly selected region had exactly two hits.