Answer:
Approximately
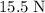 , assuming that
, assuming that
 .
.
Step-by-step explanation:
To find the tension in the rope on the right side of the pulley, apply the following steps:
- Find the tension that the rope exerts on the block, which is equal to the tension
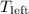 on the left side of the pulley.
on the left side of the pulley. - Find the torque
 resulting from the tension
resulting from the tension
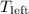 on the left side of the pulley.
on the left side of the pulley. - Find the moment of inertia
 of the pulley and the net torque
of the pulley and the net torque
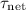 .
. - Add the torque on the left
 to the net torque
to the net torque
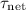 to find
to find
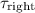 , the torque on the right side of the pulley.
, the torque on the right side of the pulley. - Divide
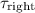 by radius of the pulley
by radius of the pulley
 to find the tension on the right side,
to find the tension on the right side,
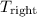 .
.
The net force on the block is:
 , where
, where
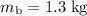 is the mass of the block, and
is the mass of the block, and
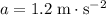 is the linear acceleration of the block.
is the linear acceleration of the block.
At the same time, the net force on the block can also be expressed as:
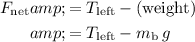 , where
, where
 by assumption, and
by assumption, and
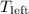 is the tension the rope exerted on the block. This tension is equal to the tension on the left side of the pulley.
is the tension the rope exerted on the block. This tension is equal to the tension on the left side of the pulley.
Rearrange and solve for
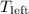 :
:
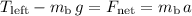 .
.
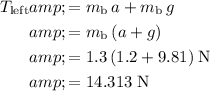 .
.
Let
 denote the radius of the pulley. It is given that the diameter of the pulley is
denote the radius of the pulley. It is given that the diameter of the pulley is
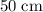 . In standard units, the radius of the pulley would be
. In standard units, the radius of the pulley would be
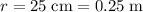 .
.
On the left side of the pulley, tension in the rope exerts a torque of
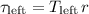 on the pulley:
on the pulley:
 .
.
Under the assumptions, the moment of inertia
 of this cylindrical pulley would be:
of this cylindrical pulley would be:
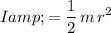 , where
, where
 is the mass of the pulley, and
is the mass of the pulley, and
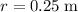 is the radius of the pulley.
is the radius of the pulley.
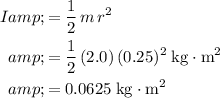 .
.
Since the rope doesn't slip on the pulley, linear acceleration of the pulley would be equal to that of the rope,
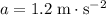 . Divide this linear acceleration by the radius of the pulley to find the angular acceleration
. Divide this linear acceleration by the radius of the pulley to find the angular acceleration
 of the pulley:
of the pulley:
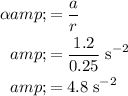 .
.
Multiply angular acceleration by the moment of inertia to find the net torque
 on the pulley cylinder:
on the pulley cylinder:
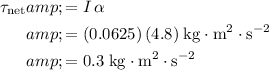 .
.
Note that the net torque of the pulley
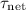 is in the same direction as
is in the same direction as
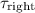 , but the opposite of
, but the opposite of
 . Hence:
. Hence:
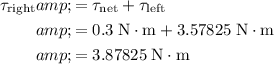 .
.
Divide the torque on the right
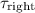 by radius
by radius
 to find the tension in the string on the right
to find the tension in the string on the right
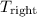 :
:
 .
.