Question

Can you solve this question?
y=?
(?,?)

Answer 1

The tangent line is: y = 8x - 58

The tangent point is at (7, -2)

===================================================

Step-by-step explanation:

One of the definitions of derivatives is

`\displaystyle f'(a) = \lim_(x\to a) (f(x)-f(a))/(x-a)`

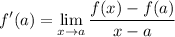
where f ' (a) represents the derivative evaluated at x = a.

The value of f ' (a) will get us the slope of the tangent at x = a.

The idea is that x is getting closer and closer to 'a'. In doing so, the secant lines slowly approach the tangent line.

Keep in mind that x will never reach 'a' itself (if it did, then we'd have a division by zero error).

---------------

The given limit we have is

`\displaystyle \lim_(x\to 7) (f(x)+2)/(x-7) = 8`

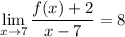
and that is equivalent to

`\displaystyle \lim_(x\to 7) (f(x)-(-2))/(x-7) = 8`

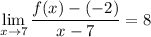
and also equivalent to

`\displaystyle \lim_(x\to 7) (f(x)-f(7))/(x-7) = 8`

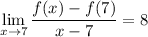
Compare that to the template I mentioned at the top to see that

• a = 7
• f(a) = f(7) = -2
• f ' (a) = f ' (7) = 8

Therefore, we can say the tangent slope is 8 and the tangent touches the f(x) curve at (x,y) = (a, f(a)) = (7,f(7)) = (7,-2)

---------------

`m = 8 = \text{slope}\\\\(x_1,y_1) = (7,-2) = \text{tangent point}\\\\`

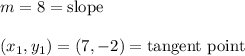
Let's use that info to determine the equation of the tangent line.

I'll use point-slope form to isolate y.

`y-y_1 = m(x-x_1)\\\\y-(-2) = 8(x-7)\\\\y+2 = 8x-56\\\\y = 8x-56-2\\\\y = 8x-58\\\\`

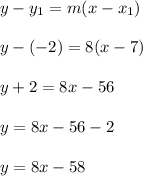
That's the equation of the tangent line to the point (7,-2).