Question

CALC PLEASE HELP!!

Let f(x)= x³ - 27x.
(i) Find the domain of f(x).
(ii) Compute f'(x) and f"(x).
(iii) Give the coordinates of the critical points.
(iv) Find the intervals where f(x) is increasing / decreasing.
(v) Give the coordinates of the relative extrema. Classify each extrema as a relative maximum
or a relative minimum.
ALSO
(vi) Find the intervals where f(x) is concave up/ concave down.
(vii) Give the coordinates of any points of inflection.
(viii) Sketch the graph of f(x).

Answer 1

Explanation:

y = x³ - 27x

(i). Domain: x ∈ ( - ∞ , ∞ )

(ii). f'(x) = 3x² - 27 ; f''(x) = 6x

(iii). 3x² - 27 = 0 ⇔ x² - 9 = 0 ⇒
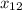`x_(12)` = ± 3

If
`x_(1)` = - 3 , then
`y_(1)` = 54

If
`x_(2)` = 3 , then
`y_(1)` = - 54

Points are ( - 3 , 54 ) and ( 3 , - 54 )

(iv). ( - ∞ , - 3 ) ∪ ( - 3 , 3 ) ∪ ( 3 , ∞ )

increasing ----> decreasing -----> increasing

(v). x = - 3 is the maxima, the local maximum value is 54, f(-3) = 54

x = 3 is the minima, the local minimum value is ( - 54 ), f(3) = - 54

(vi). Concave up if f''(x) > 0 ; The interval is ( - ∞ , 0 )

Concave down if f''(x) < 0 ; The interval is ( 0 , ∞ )

(vii). Point of inflection is ( 0 , 0 )

f''(x) = 0

6x = 0

x = 0