Question

A truck with 38-in.-diameter wheels is traveling at 60 mi/h.

Find the angular speed of the wheels in rad/min: rad/min

How many revolutions per minute do the wheels make?

Answer 1

• 530.7 rpm
• 3334.7 rad/min

Explanation:

You want the angular speed in RPM and in radians per minute for a truck wheel 38 inches in diameter traveling at 60 mph.

Revolutions

There are 60 minutes in an hour, so a speed of 60 mi/h is a speed of ...

`\frac{60\text{ mi}}{1\text{ h}}*\frac{1\text{ h}}{60\text{ min}}*\frac{5280\text{ ft}}{1\text{ mi}}=5280\text{ ft/min}`

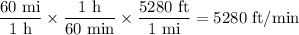
The distance traveled for 1 revolution of the wheel is equal to its circumference:

C = πd

C = π(38 in)/(12 in/ft) = (19/6)π ft ≈ 9.948 ft

Then the number of revolutions in 5280 ft is ...

(5280 ft/min)/(9.948 ft/rev) ≈ 530.7 rev/min

The wheels make about 530.7 revolutions per minute.

Radians

Each revolution is an angle of 2π radians, so the angular speed is ...

ω = 530.7 rev/min × 2π rad/rev

ω = 3334.7 rad/min