Question

Question
Solve the equation. Check your solutions.

∣x−7∣=∣2x−8∣

Answer 1

x = 1, x = 5

Explanation:

You want the solutions to the absolute value equation ...

|x -7| = |2x -8|

Piecewise equation

Each of the absolute value functions is equivalent to a piecewise-defined function. The boundary for the pieces is the turning point of the absolute value function, where its argument is zero.

The turning points are ...

x -7 = 0 ⇒ x = 7

2x -8 = 0 ⇒ x = 8/2 = 4

This means the equivalent piecewise equation will have 3 pieces. We know the absolute value function is defined as ...

`|x|=\begin{cases}-x&\text{for }x < 0\\x&\text{for }x\ge0\end{cases}`

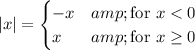
If we write the equation in the form |x -7| - |2x -8| = 0, we have ...

`0=\begin{cases}-(x-7)-(-(2x-8))&\text{for }x < 4\\-(x-7)-(2x-8)&\text{for }4\le x < 7\\(x-7)-(2x-8)&\text{for }7\le x\end{cases}`

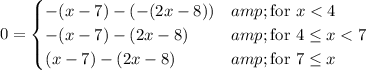
x < 4

The equation simplifies to ...

-x +7 +2x -8 = 0

x -1 = 0 . . . . collect terms

x = 1 . . . . . . a value in the domain. This is one solution.

4 ≤ x < 7

The equation simplifies to ...

-x +7 -2x +8 = 0

15 = 3x . . . . . . . . . . add 3x

5 = x . . . . . . . . a value in the domain. This is another solution

7 ≤ x

The equation simplifies to

x -7 -2x +8 = 0

-x +1 = 0

x = 1 . . . . . . . . . not in the domain 7 ≤ x, so not a solution

The solutions are x = 1 and x = 5.

__

Check

|1 -7| = |2·1 -8| ⇒ |-6| = |-6| . . . . true

|5 -7| = |2·5 -8| ⇒ |-2| = |2| . . . . true

Both solutions check in the original equation.