Question

a 1.3-kg block is attached to the end of a 1.7-m string to form a pendulum. the pendulum is released from rest when the string is horizontal. at the lowest point of its swing when it is moving horizontally, the block is hit by a 0.01-kg bullet moving horizontally in the opposite direction. the bullet remains in the block and causes the block to come to rest at the low point of its swing. what was the magnitude of the bullet's velocity just before hitting the block?

Answer 1

Given Information:

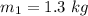`m_(1)=1.3 \ kg` (Mass of the block attached to the pendulum)

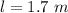`l=1.7 \ m` (Length of the string)

`m_(b)=0.01 \ kg` (Mass of the bullet)

Information we want to Find:

`||\vec v_(b) || = ?? \ m/s`

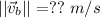
Concepts/Equations used:

Using the idea of momentum, momentum conservation, and energy conservation to solve.

Momentum =>
`\vec p=m \vec v`

Momentum Conservation =>
`\vec p_(0) = \vec p_(f)`

Energy Conservation =>
`E_(0) = E_(f)`

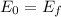
Finding the blocks velocity at the bottom of its swing using conservation of energy. Analyzing points 1 and 2 (Refer to the attached image).

Energy at point 1...

The energy at point 1 is all gravitational potential energy, where
`U_(g) =m_(1) gl`.

`\Longrightarrow U_(g) =m_(1) gl`

`\Longrightarrow U_(g) =(1.3)(9.8)(1.7)`

`\Longrightarrow U_(g) =(1.3)(9.8)(1.7)`

`\Longrightarrow U_(g) = 21.658 \ J`

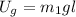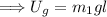
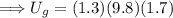
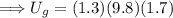
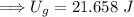
Thus,
`E_(0)= 21.658 \ J`.

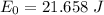Now for the energy at point 2...

The energy at point 1 is all kinetic, where
`K=(1)/(2)m_(1)v^(2) _(f)`.

`\Longrightarrow K=(1)/(2)m_(1)v^(2) _(f)`

`\Longrightarrow K=(1)/(2)(1.3)v^(2) _(f)`

`\Longrightarrow K=0.65v^(2) _(f)`

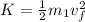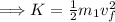
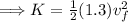
Thus,
`E_(f)=0.65v^(2) _(f)`.

`E_(0) = E_(f)`

`\Longrightarrow 21.658 = 0.65v^(2) _(f)`

`\Longrightarrow v^(2) _(f)=33.32`

`\Longrightarrow v _(f)=√(33.32)`

`\Longrightarrow v_(f) = 5.77 \ m/s`

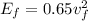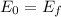
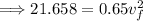
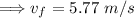
The momentum of the block at point 2,
`\vec p =m_(1) \vec v_(f)`.

`\vec p_(block) =m_(1) \vec v_(f)`

`\Longrightarrow \vec p_(block) =(1.3) (5.77)`

`\Longrightarrow \vec p_(block) = 7.50 \ Ns`

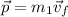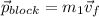
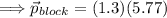
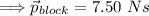
For the block to stop the momentum of the bullet must equal the momentum of the moving block.

`\vec p_(0) = \vec p_(f) = > \vec p_(bullet) = \vec p_(block)`

`\Longrightarrow m_(b) \vec v_(b) = 7.5`

`\Longrightarrow (0.01) \vec v_(b) = 7.5`

`\Longrightarrow \vec v_(b) = 750 \ m/s`

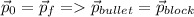
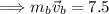
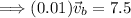
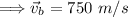
Thus, the bullet was travelling 750m/s before hitting the block.