Question

what is the final velocity (in m/s) of a hoop that rolls without slipping down a 6.50-m-high hill, starting from rest?

Answer 1

Approximately
`7.99\; {\rm m\cdot s^(-1)}`.

(Assuming that
`g = 9.81\; {\rm N \cdot kg^(-1)}` and that the thickness of the loop is negligible.)

Step-by-step explanation:

Let
`m` denote the mass of the hoop, and let
`r` denote its radius.

Under the assumptions, the moment of inertia of this hoop would be:

`\displaystyle I = m\, r^(2)`.

Let
`v` denote the linear velocity of the hoop at the bottom of the hill. The linear kinetic energy of the hoop would be:

`\displaystyle (1)/(2)\, m\, v^(2)`.

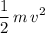Since the hoop is rolling without slipping, its angular velocity would be
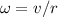`\omega = v / r`. The rotational kinetic energy of the hoop would be:

`\begin{aligned}(1)/(2)\, I\, \omega^(2) &= (1)/(2)\, (m\, r^(2))\, \left((v)/(r)\right)^(2) \\ &= (1)/(2)\, (m\, r^(2)\, v^(2))/(r^(2)) \\ &= (1)/(2)\, m\, v^(2)\end{aligned}`.

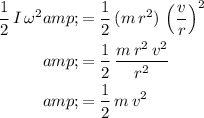The total kinetic energy of the hoop (linear and rotational) would be:

`\begin{aligned}& (1)/(2)\, m\, v^(2) + (1)/(2)\, I\, \omega^(2) \\ =\; & (1)/(2)\, m\, v^(2) + (1)/(2)\, m\, v^(2) \\ =\; & m\, v^(2) \end{aligned}`.

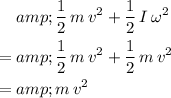Assuming that total mechanical energy is conserved. Change in the Kinetic energy that the loop has gained would be the opposite of the change in the gravitational potential energy (GPE):

`\begin{aligned}(\text{change in GPE}) &= m\, g\, \Delta h\end{aligned}`,

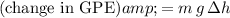Where:

• 
  `g = 9.81\; {\rm N\cdot kg^(-1)}` by assumption, and
• 
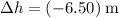  `\Delta h = (-6.50)\; {\rm m}` is the change in the height of the hoop.

By the conservation of energy:

`(\text{change in KE}) + (\text{change in GPE}) = 0`.

`m\, v^(2) + m\, g\, \Delta h = 0`.

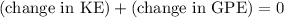Solve for
`v`:

`\begin{aligned}m\, v^(2) &= m\, g\, (-\Delta h)\end{aligned}`.

`\begin{aligned}v &= √(g\, (-\Delta h)) \\ &= √((9.81)\, (-(-6.50)))\; {\rm m\cdot s^(-1)} \\ &\approx 7.99\; {\rm m\cdot s^(-1)}\end{aligned}`.

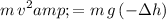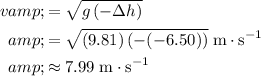In other words, the velocity of the loop would be approximately
`7.99\; {\rm m\cdot s^(-1)}` at the bottom of the hill.