Question

Which best describes the relationship between the line that passes through the points (–6, 5) and (–2, 7) and the line that passes through the points (4, 2) and (6, 6)?

A. same line
B. neither perpendicular nor parallel
C. parallel
D. perpendicular

Answer 1

B

Explanation:

calculate the slopes m of the 2 lines using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

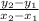
with (x₁, y₁ ) = (- 6, 5 ) and (x₂, y₂ ) = (- 2, 7 )

m =
`(7-5)/(-2-(-6))` =
`(2)/(-2+6)` =
`(2)/(4)` =
`(1)/(2)`

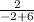repeat with

(x₁, y₁ ) = (4, 2 ) and (x₂, y₂ ) = (6, 6 )

m =
`(6-2)/(6-4)` =
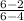`(4)/(2)` = 2

• Parallel lines have equal slopes

`(1)/(2)` ≠ 2 , then lines are not parallel

the product of the slopes of perpendicular lines equals - 1

`(1)/(2)` × 2 = 1 ≠ - 1 , thus lines are not perpendicular

the lines are neither perpendicular nor parallel