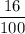P(inside larger square and outside smaller) =
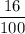
Step-by-step explanation:
Probability is the result of the division of the number of possible outcome by the number of an event.
In the question, for a point chosen, the point can be in the small square only or in the area or region between the small square and the big square as such,
Area of larger square = area of region between both squares + area of smaller square
Where the area of a square is S × S where S is the side of a square
Area of larger square = 5 × 5
= 25 cm square
Area of smaller square = 3 × 3
= 9 cm square
Area of the region between both squares
= 25 - 9
= 16 cm square
The probability that a dot selected is inside the larger square and outside the smaller is
P(inside larger square and outside smaller) = Area of region between both square/ Area of larger square
P(inside larger square and outside smaller) =