Brittany's first mistake is in step 3. She incorrectly simplifies the expression
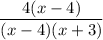 to
to
 . The correct simplification is
. The correct simplification is
 .
.
Brittany's first mistake is in Step 3. She incorrectly simplifies the expression
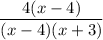 to
to
 . The correct simplification is
. The correct simplification is
 .
.
Here is a step-by-step explanation of Brittany's error:
Step 2:
=
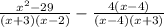
Step 3:
=
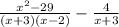
Brittany's mistake: In this step, Brittany cancels the x-4 factor from the numerator and denominator of the second term. This is incorrect because the x-4 factor is not present in the denominator of the first term.
Correct simplification:
=
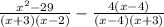
=
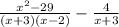
If Brittany had correctly simplified the expression in Step 3, her subsequent steps would have been correct. The correct difference in simplest form is therefore:
=
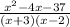
Answers:
Step at which Brittany made her first mistake: Step 3
Correct difference in simplest form:
