Question

What is the equation of the line that passes through (-1,-10) and (3,14)

Answer 1

6x - y - 4 = 0

Explanation:

To find:-

• The equation of the line passing through the points (-1,-10) and (3,14) .

Solution:-

We are here given two lines and we are interested in finding out the equation of the line passing through the given points.

Firstly here we will find out the slope of the line as ,

`:\implies \sf m =(y_2-y_1)/(x_2-x_1)\\`

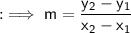
Now on substituting the respective values, we have;

`:\implies \sf m =(-10-14)/(-1-3) \\`

`:\implies \sf m = (-24)/(-4)\\`

`:\implies \sf\pink{ m = 6}\\`

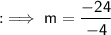
Now we can use the point slope form of the line to find out the equation of the line . The point slope form of the line is ,

`:\implies \sf \pink{ y - y_1 = m(x_2-x_1)}\\`

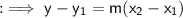
Take any one of the given points for (x₁,y₁) . Here i am taking (3,14) .

Now finally substitute the respective values,

`:\implies \sf y - 14= 6(x -3 )\\`

`:\implies \sf y- 14= 6x - 18 \\`

`:\implies \sf 6x - y - 18 + 14 = 0\\`

`:\implies \sf\pink{ 6x - y -4 = 0 }\\`

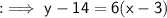
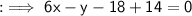
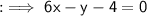
Hence the required equation of the line in standard form is 6x - y - 4 = 0 .

Answer 2

`y = 6x - 4`

Explanation:

To find the equation of the line that passes through the given points (-1, -10) and (3, 14), first find the slope by inputting the points into the slope formula.

`\boxed{\begin{minipage}{8cm}\underline{Slope Formula}\\\\Slope $(m)=(y_2-y_1)/(x_2-x_1)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.\\\end{minipage}}`

Let (x₁, y₁) = (-1, -10)

Let (x₂, y₂) = (3, 14)

Therefore, the slope of the equation is:

`\implies m=(14-(-10))/(3-(-1))=(14+10)/(3+1)=(24)/(4)=6`

Now that we have determined the slope of the line, we can input the found slope and either of the two given points into the point-slope formula to create the equation of the line.

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Substituting m = 6 and (x₁, y₁) = (-1, -10) into the point-slope formula:

`\implies y-(-10)=6(x-(-1))`

Simplifying:

`\implies y+10=6(x+1)`

`\implies y+10=6x+6`

`\implies y=6x-4`

Therefore, the equation of the line that passes through (-1,-10) and (3,14) is:

`\boxed{y = 6x - 4}`