Answer:
The interest rate is 5.79% (to the nearest hundredth).
Explanation:
To find the interest rate for the given deposit of $4000 accumulating to $5994.75, compounded monthly for 7 years, use the compound interest formula.
Compound Interest Formula
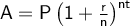
where:
- A = Final amount.
- P = Principal amount.
- r = Interest rate (in decimal form).
- n = Number of times interest is applied per year.
- t = Time (in years).
Given values:
- P = $4,000
- A = $5,994.75
- n = 12 (monthly)
- t = 7 years
Substitute the given values into the formula and solve for r.
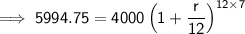
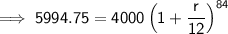
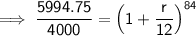
![\implies \sf \sqrt[\sf 84]{\sf (5994.75)/(4000)}=1+(r)/(12)](https://img.qammunity.org/2024/formulas/mathematics/college/c32um8f40mr6y0sptc0htodh0ycotneoxk.png)
![\implies \sf \sqrt[\sf 84]{\sf (5994.75)/(4000)}-1=(r)/(12)](https://img.qammunity.org/2024/formulas/mathematics/college/2oxhohw5103vfiq6uhgkgscsq3ebwws6zi.png)
![\implies \sf r=12\left(\sqrt[\sf 84]{\sf (5994.75)/(4000)}-1\right)](https://img.qammunity.org/2024/formulas/mathematics/college/s8on02myv6fo4w753usyr4cnsxpv3mxn0l.png)
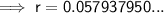
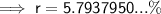
Therefore, the interest rate is 5.79% (to the nearest hundredth).