Question

A radio station has a broadcast area in the shape of a circle with equation x^2+y^2=5,625, where the constant represents square miles.

a. Find the intercepts of the graph.
b. State the radius in miles.
c. What is the area of the region in which the broadcast from the station can be picked up?
Show all work please!!

Answer 1

• (75,0) ; (-75,0) ; (0,75) ; (0,-75)
• 75 miles
• 17678.51 miles²

Explanation:

To find:-

• The intercepts of the graph .
• Radius in miles.
• Area of the region.

Answer:-

The given equation of the circle is ,

`:\sf\implies x^2 + y^2 = 5625 \\`

`\rule{200}2`

G R A P H : -

`\setlength{\unitlength}{7mm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\vector(1,0){6}}\put(0,0){\vector(-1,0){6}}\put(0,0){\vector(0,1){6}}\put(0,0){\vector(0,-1){6}}\put(.2,2.5){$\sf (0,75)$}\put(.2, - 2.7){$\sf (0,-75)$}\put(2.5,0.2){$\sf (75,0)$}\put( - 4.2,.2){$\sf ( - 75,0)$}\put(4,4){$\bigstar \: \: \sf Centre = (0,0) $}\put(4,3){$\bigstar \: \: \sf Radius = 75\ miles $}\put(4,-4){$\boxed{\bf \textcopyright \: \: Tony Stark }$}\end{picture}`

`\rule{200}2`

Answer a :-

The intercepts are the points at which the circle cuts the x-axis and y-axis . At x intercept , the value of y coordinate becomes 0 and at y intercept the x coordinate becomes 0 .

So for finding x intercept , plug in y = 0 , in the given equation of circle, as ;

`:\sf\implies x^2 + (0)^2 = 5625 \\`

`:\sf\implies x^2 = 5625 \\`

`:\sf\implies x =√(5625) \\`

`:\sf\implies x =\pm 75 \\`

`:\sf\implies \red{ x = +75 , -75} \\`

Hence the circle cuts the x-axis at (75,0) and (-75,0).

To find out y intercept plug in x = 0 in the given equation of the circle as ,

`:\sf\implies (0)^2 + y^2 = 5625 \\`

`:\sf\implies y^2 = 5625 \\`

`:\sf\implies y=√(5626)\\`

`:\sf\implies y = \pm 75 \\`

`:\sf\implies \red{ y = +75,-75} \\`

Hence the circle cuts the y-axis at (0,75) and (0,-75).

`\rule{200}2`

Answer b :-

Next we are interested in finding out the radius of the circle, for that we need to compare the given equation of circle to the standard equation of circle .

Standard equation of circle :-

`:\sf\implies \red{ (x-h)^2 + (y-k)^2 = r^2}`

where ,

• (h,k) is the centre of the circle.
• r is the radius.

We can rewrite the given equation of circle as ,

`:\sf\implies (x-0)^2 + (y-0)^2 = 5625 \\`

`:\sf\implies (x-0)^2+(y-0)^2 = 75^2\\`

On comparing to the standard form, we have;

`:\sf\implies \red{ radius = 75\ miles } \\`

Hence the radius of the circle is 75miles .

`\rule{200}2`

Answer c :-

To find out the area we can use the formula of area of circle , which is ;

`:\sf\implies \red{Area=\pi(radius)^2} \\`

We already got the radius to be 75 miles in the previous part of the question. Plugging in that value would give us the area , as ;

`:\sf\implies Area =\pi (75\ miles )^2 \\`

`:\sf\implies Area = (22)/(7)* 5625\ miles^2\\`

`:\sf\implies \red{ Area = 17678.57 \ miles^2 } \\`

Hence the area of the circle is 17678.57 miles² .

Answer 2

a) The intercepts of the graph are (-75, 0), (75, 0), (0, -75) and (0, 75).

b) The radius is 75 miles.

c) The area of the region is 17,671 square miles (to the nearest square mile).

Explanation:

Part a

The x-intercepts are the points at which the graph crosses the x-axis, so when y = 0. Therefore, to find the x-intercepts, substitute y = 0 into the given equation.

`\implies x^2+y^2=5625`

`\implies x^2+(0)^2&=5625`

`\implies x^2&=5625`

`\implies x&=√(5625)`

`\implies x&=\pm75`

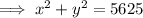
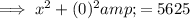
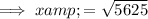
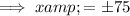
The y-intercepts are the points at which the graph crosses the y-axis, so when x = 0. Therefore, to find the y-intercepts, substitute x = 0 into the given equation.

`\implies x^2+y^2=5625`

`\implies (0)^2+y^2&=5625`

`\implies y^2&=5625`

`\implies y&=√(5625)`

`\implies y&=\pm75`

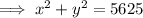
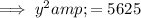
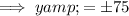
Therefore, the intercepts of the graph are:

• (-75, 0), (75, 0), (0, -75) and (0, 75)

`\hrulefill`

Part b

The general equation of a circle is:

`(x-h)^2+(y-k)^2=r^2`

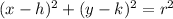
where (h, k) is the center and r is the radius of the circle.

By comparing the given equation with the general equation:

• (h, k) = (0, 0)
• r² = 5625

Take the positive square root of r² to find the radius of the circle (since length cannot be negative):

`\implies r=√(5625)`

`\implies r=75`

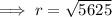
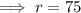
Therefore, the radius of the circle is 75 miles.

`\hrulefill`

Part c

The formula for the area of a circle is:

`A=\pi r^2`

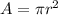
where r is the radius.

To find the area of the region in which the broadcast from the station can be picked up, find the area of the circle with the radius from part b, r = 75:

`\implies A= \pi \cdot 75^2`

`\implies A=5625 \pi`

`\implies A=17671.4586...`

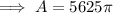
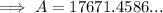
Therefore, the area of the region is 17,671 square miles (to the nearest square mile).