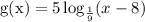Question

F(x) = log1/9x; translation 8 units right followed by a vertical stretch by a factor of 5

A) g(x)=5log1/9(x-8)
B) g(x)=log1/9 5x-8
C) g(x) log1/9 (5x-8)
D) g(x) 5log1/9 x-40

Answer 1

Answer: its 7

Explanation:

its 7

Answer 2

The transformed equation of the function f(x) is
`\text{g(x)} = 5\log_{(1)/(9)}(x - 8)`

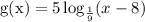
How to determine the transformed equation

From the question, we have the following parameters that can be used in our computation:

`\text{f(x)} = \log_{(1)/(9)}(x)`

Also, we have the sequence of transformations to be

• A translation 8 units right
• A vertical stretch by a factor of 5

The translation is represented as

(x, y) = (x - 8, y)

So, we have

`\text{f(x)} = \log_{(1)/(9)}(x - 8)`

The vertical stretch is represented as

(x, y) = (x, 5y)

So, we have

`\text{g(x)} = 5\log_{(1)/(9)}(x - 8)`

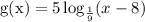
Hence, the transformed equation is
`\text{g(x)} = 5\log_{(1)/(9)}(x - 8)`