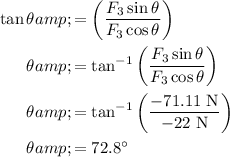Question

- An object in equilibrium has three forces exerted on it. A 33-N force act at 90° from the x-axis and a 46-N force act at 60°. What are the magnitude and direction of the third force

Answer 1

Step-by-step explanation:

The 33 N force is at a 90 degree angle, whereas the 44 N force is at a 60 degree angle with the x-axis.

Assume that the third force makes a theta-angle contact with the x-axis.

Since the object is in balance, the total force acting on it will equal zero.

Find the accumulation of the x-axis forces.

`\begin{aligned} 33\cos 90{}^\circ +44\cos 60{}^\circ +{{F}_(3)}\cos \theta &=0 \\ 0+22\text{ N}+{{F}_(3)}\cos \theta &=0 \\ {{F}_(3)}\cos \theta &=-22\text{ N }......\text{ }\left( 1 \right) \end{aligned}`

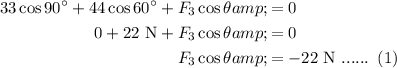
Find accumulation of the y-axis forces.

`\begin{aligned} 33\sin 90{}^\circ +44\sin 60{}^\circ +{{F}_(3)}\sin \theta &=0 \\ 33\text{ N}+38.11\text{ N}+{{F}_(3)}\sin \theta &=0 \\ {{F}_(3)}\sin \theta &=-71.11\text{ N }......\text{ }\left( 2 \right) \end{aligned}`

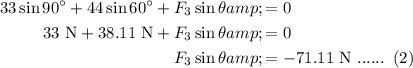
Identify the magnitude.

`\begin{aligned} F&=\sqrt{{{\left( {{F}_(3)}\cos \theta \right)}^(2)}+{{\left( {{F}_(3)}\sin \theta \right)}^(2)}} \\ &=\sqrt{{{\left( -22\text{ N} \right)}^(2)}+{{\left( -71.11\text{ N} \right)}^(2)}} \\ &=74.43\text{ N} \end{aligned}`

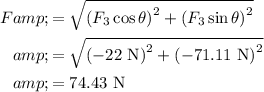
Identify the direction.

`\begin{aligned} \tan \theta &=\left( \frac{{{F}_(3)}\sin \theta }{{{F}_(3)}\cos \theta } \right) \\ \theta &={{\tan }^(-1)}\left( \frac{{{F}_(3)}\sin \theta }{{{F}_(3)}\cos \theta } \right) \\ \theta &={{\tan }^(-1)}\left( \frac{-71.11\text{ N}}{-22\text{ N}} \right) \\ \theta &=72.8{}^\circ \end{aligned}`