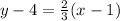Question

The line perpendicular to y= (-3/2)x -4 and goes through (1,4)

Answer 1

Answer (assuming it is allowed to be in point-slope format):

`y-4 = (2)/(3)(x-1)`

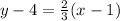
Explanation:

1) First, determine the slope. We know it has to be perpendicular to the given equation,
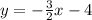`y = -(3)/(2) x-4`. That equation is already in slope-intercept form, or y = mx + b format, in which m represents the slope. Since
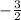`-(3)/(2)` is in place of the m in the equation, that must be the slope of the given line.

Slopes that are perpendicular are opposite reciprocals of each other (they have different signs, and the denominators and numerators switch places). Thus, the slope of the new line must be
`(2)/(3)`.

2) Now, use the point-slope formula,
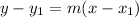`y-y_1 = m (x-x_1)` to write the new equation with the given information. Substitute
`m`,
`x_1`, and
`y_1` for real values.

The
`m` represents the slope, so substitute
`(2)/(3)` in its place. The
`x_1` and
`y_1` represent the x and y values of a point the line intersects. Since the point crosses (1,4), substitute 1 for
`x_1` and 4 for
`y_1`. This gives the following equation and answer:

`y-4 = (2)/(3)(x-1)`