Question

Cos² (x)(1+tan²(x)) = 1, establish the identity

Answer 1

see below.

Explanation:

Use Trigonometric Expansion.

Verify the following identity:

`cos(x)^2(tan(x)^2+1)=1`

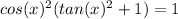
Write tangent as
`(sine)/(cosine)`

`cos(x)^2((sin(x))/(cos(x)) ^2+1)=1`

`cos(x)^2((sin(x))/(cos(x)) ^2+1)=cos(x)^2((sin(x)^2)/(cos(x)^2+1) )`

`(cos(x)^2((sin(x)^2)/(cos(x)^2) +1))=1`

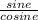
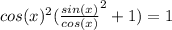
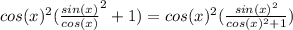
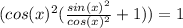
Put sin(x)^2/cos(x)^2 +1 over the common denominator cos(x)^2 : sin(x)^2/cos(x)^2+1 = cos(x)^2+sin(x)^2 /cos (x)^2:

cos(x)^2(cos(x)^2+sin(x)^2/cos(x)^2)=1

Cancel cos(x)^2 from the numerator to the denominator.

cos(x)^2(cos(x)^sin(x)^2)/cos(x)^2=cos(x)^2(cos(x)^2+sin(x)^2)/cos(x)^2=cos(x)+sin(x)^2:

(cos(x)^2+sin(x)^2=1

Substitute cos(x)^2 + sin (x)^2 = 1:

1 =1