Answer:
x = 48.6°
Explanation:
We are heree given a right angled triangle in which we are interested in finding the value of unknown angle " x " . with respect to angle x , HG is perpendicular and FH is hypotenuse. Also , in right angled triangle, sine is defined as the ratio of perpendicular and hypotenuse.
So that ,
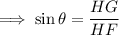
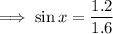
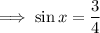
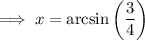
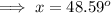
Rounding to nearest tenth,
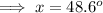
Hence the value of x is 48.6° .