Question

Find the least common factor of 12 and 36

Answer 1

36

Explanation:

The LCM, or Least Common Multiple, of two or more numbers is the smallest value that all the numbers considered can be divided into evenly. So, the LCM of 12 and 36 would be the smallest number that can be divided by both 12 and 36 exactly, without any remainder left afterwards.

How to find the LCM of 12 and 36 using Prime Factorization

One way to find the LCM of 12 and 36 is to start by comparing the prime factorization of each number. To find the prime factorization, you can follow the instructions for each number here:

Here is the prime factorization of 12:

`2^(2)` ·
`3^(1)`

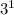
And this is the prime factorization of 36:

`2^(2)` ·
`3^(2)`

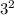
When you compare the prime factorization of these two numbers, you want to look for the highest power that each prime factor is raised to. In this case, there are these prime factors to consider: 2, 3

`2^(2)` ·
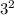`3^(2)` = 36

Through this we see that the LCM of 12 and 36 is 36.