Question

[Use g = 10 m/s2]

A box of mass 60 kg slides down a frictionless 30° incline a distance d = 4 meters, striking a spring. The spring compresses an additional distance x = 1 meters before the box comes momentarily to rest. What is the force constant of the spring?

Answer 1

`3000\; {\rm N\cdot m^(-1)}`.

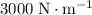Step-by-step explanation:

In this question, the box has travelled a total run of
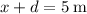`x + d = 5\; {\rm m}` along the incline. It is given that the angle of elevation is
`\theta = 30^(\circ)` for this incline. The change in the height (rise) of the box would be:

`\begin{aligned}\Delta h &= (\text{run})\, \frac{\text{rise}}{\text{run}} \\ &= (\text{run})\, \sin(\theta) \\ &= (5)\, \sin(30^(\circ))\; {\rm m} \\ &= (5)/(2)\; {\rm m}\end{aligned}`.

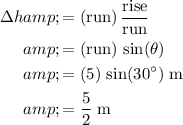In other words, the height of the box would have changed by
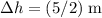`\Delta h = (5/2)\; {\rm m}`. The change in the gravitational potential energy (GPE) of the box would be:

`\begin{aligned}(\text{GPE}) &= m\, g\, \Delta h \end{aligned}`.

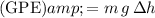In this equation:

• 
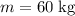  `m = 60\; {\rm kg}` is the mass of the box, and
• 
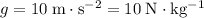  `g = 10\; {\rm m\cdot s^(-2)} = 10\; {\rm N\cdot kg^(-1)}` is the gravitational field strength.

When the spring is at maximum compression, elastic potential energy (EPE) in the spring would be:

`\begin{aligned}(\text{EPE}) &= (1)/(2)\, k\, x^(2)\end{aligned}`,
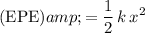In this equation:

• 
  `k` is the spring constant, and
• 
  `x = 1\; {\rm m}` is the displacement of the spring.

Since the incline is frictionless, all the GPE of the block would have been converted into the EPE of the spring:

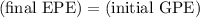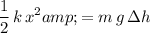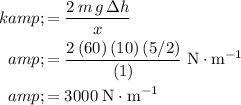`\begin{aligned}(\text{final EPE}) = (\text{initial GPE})\end{aligned}`.

`\begin{aligned}(1)/(2)\, k\, x^(2) &= m\, g\, \Delta h \end{aligned}`.

`\begin{aligned}k &= (2\, m\, g\, \Delta h)/(x) \\ &= (2\, (60)\, (10)\, (5/2))/((1))\; {\rm N\cdot m^(-1)} \\ &= 3000\; {\rm N\cdot m^(-1)}\end{aligned}`.