Question

If you deposit $25,000 now at 6.5% compounded quarterly, how much will you have in 30 years?

Answer 1

A=25000(1+0.065/1)^4•30
A=25000•1.01625^120
A=25000•6.919378
A= $172984.45

In 30 years you will have $172984.45

Answer 2

$172,984.44 (nearest cent)

Explanation:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given:

• P = $25,000
• r = 6.5% = 0.065
• n = 4 (quarterly)
• t = 30 years

Substitute the given values into the formula and solve for A:

`\implies A=25000\left(1+(0.065)/(4)\right)^(4 \cdot 30)`

`\implies A=25000\left(1.01625\right)^(120)`

`\implies A=25000\left(6.9193776...\right)`

`\implies A=172984.4404`

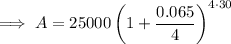
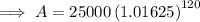
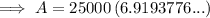
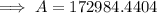
Therefore, if you deposit $25,000 now at 6.5% compounded quarterly, you will have $172,984.44 (nearest cent) in 30 years.