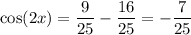Question

Find the exact value pf cos 2x if sin x = - 4/5 (Quadrant III)

Answer 1

`\displaystyle \cos(2x)=-(7)/(25)`

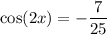
Explanation:

We want to find:

`\displaystyle \cos(2x)\text{ given that }\sin(x)=-(4)/(5)`

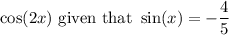
And x is in QIII.

Recall that sine is the ratio of the opposite side to the hypotenuse.

Therefore, the adjacent side is (we can ignore the negative for now).

`a=√(5^2-4^2)=√(25-16)=√(9)=3`

So, the adjacent side is 3, the opposite side is 4, and the hypotenuse is 5.

Using the double angle identity, we can rewrite:

`\cos(2x)=\cos^2(x)-\sin^2(x)`

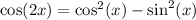
Since x is in QIII, cosine is positive, sine is negative, and tangent is negative.

Using the above values, we can conclude that:

`\displaystyle \cos(x)=(3)/(5)\text{ and } \sin(x)=-(4)/(5)`

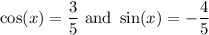
Substitute:

`\displaystyle \cos(2x)=\Big((3)/(5)\Big)^2-\Big(-(4)/(5)\Big)^2`

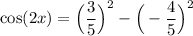
Evaluate:

`\displaystyle \cos(2x)=(9)/(25)-(16)/(25)=-(7)/(25)`