Question

1) x² + x + 3 = 0 use the discriminant to tell whether the equation has two solution​

Answer 1

The equation does not have any real solutions.

The equation only has two imaginary solutions.

Explanation:

Step 1

• Use Discriminant to check how many solutions does the equation have.

`\large{D = {b}^(2) - 4ac}`

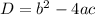
Let a = 1, b = 1 and c = 3 from the given equation.

`D = {(1)}^(2) - 4(1)(3) \\ D = 1 - 12 \\ D = - 11`

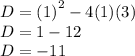
Since the value of D is in negative. Therefore, the equation does not have any solutions.

Discriminant

`D > 0 \longrightarrow \sf{two \: \: real \: \: solutions} \\ D = 0 \longrightarrow \sf{one \: \: real \: \: solution} \\ D < 0 \longrightarrow \sf{two \: \: imaginary \: \: solutions}`