Question

Solve for x
(9x-16)
(3x+11)
(7x-5)

Answer 1

The value of x is 10.

To solve for x in the given triangle, we use the fact that the sum of the interior angles of a triangle is always 180 degrees. Given the angles
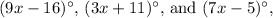`\( (9x - 16)^\circ \), \( (3x + 11)^\circ \), and \( (7x - 5)^\circ \),` we can set up an equation:

`\[ (9x - 16) + (3x + 11) + (7x - 5) = 180 \]`

Combining like terms, we get:

`\[ 9x + 3x + 7x - 16 + 11 - 5 = 180 \]`

`\[ 19x - 10 = 180 \]`

Adding 10 to both sides:

`\[ 19x = 190 \]`

Dividing both sides by 19:

`\[ x = (190)/(19) \]`

`\[ x = 10 \]`

Answer 2

`\huge\boxed{\sf x = 10}`

Explanation:

Statement:

• The measure of internal angles of a triangle adds up to 180 degrees.

Solution:

So,

(9x - 16) + (3x + 11) + (7x - 5) = 180

9x - 16 + 3x + 11 + 7x - 5 = 180

• Combine like terms

9x + 3x + 7x - 16 + 11 - 5 = 180

19x - 10 = 180

• Add 10 to both sides

19x = 180 + 10

19x = 190

• Divide both sides by 19

x = 190/19

x = 10

`\rule[225]{225}{2}`