Question

Solve for x. Round to the nearest tenth, if necessary.

Answer 1

`x = 24.4`

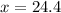
Explanation:

We arre given a right angled triangle and we are interested in solving out for " x " .

Here we can make use of trigonometric ratios for a right angled triangle.

We can see that the sides involved in the triangle are perpendicular and base therefore we can make use of ratio of tangent .

In a right angled triangle, tangent is ,

`\implies \tan\theta =(p)/(b)\\`

where,

• p is perpendicular
• b is base
• θ is the angle opposite

And here ,

• p = 19
• b = x
• θ = 38° .
• tan38° = 0.78

On substituting the respective values, we have;

`\implies \tan38^o = (19)/(x) \\`

`\implies 0.78 =(19)/(x) \\`

`\implies x = (19)/(0.78)\\`

`\implies x = 24.35 \\`

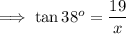
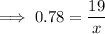
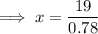
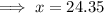
After rounding off to nearest tenth ,

`\implies \boxed{ x = 24.4} \\`

Hence the value of x is 24.4 .