Question

The sum of the squares of any two consecutive even numbers is always a multiple of which of the following? Select all of the correct answers. 2, 4, 6, 8, 10, 16​

Answer 1

The sum of the squares of any two consecutive even numbers is always a multiple of 2 and a multiple of 4.

Explanation:

An even number can be defined as 2n, where n is an integer.

Therefore, the consecutive even number can be defined as 2n+2.

So the sum of their squares is:

`\begin{aligned}(2n)^2+(2n+2)^2&=4n^2+(2n+2)(2n+2)\\&=4n^2+4n^2+4n+4n+4\\&=8n^2+8n+4\end{aligned}`

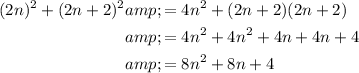
Factor out 2 from each term:

`\implies 8n^2+8n+4=2(4n^2+4n+2)`

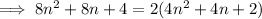
Therefore, the sum of the squares of any two consecutive even numbers is always a multiple of 2.

Factor out 4 from each term:

`\implies 8n^2+8n+4=4(2n^2+2n+1)`

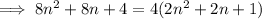
Therefore, the sum of the squares of any two consecutive even numbers is always a multiple of 4.