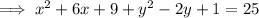Question

(Three students are sitting in a playground to make a circular path. They are sitting on the circumference, the co-ordinates of their position on the circle are (- 6, 5), (-3,- 4) and (2, 1). Find the co-ordinates of the point equidistant from their position. Also find the equation of the locus of the circular path.) Ans: x² + y² + 6x - y - 15 = 0​

Answer 1

The coordinates of the point equidistant from the position of the three students is (-3, 1).

The equation of the locus of the circular path is:

`x^2+y^2+6x-2y-15=0`

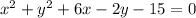
Explanation:

The point that is equidistant from the three students is the circumcenter of the triangle formed by the three students.

The circumcenter of a triangle is the point at which the perpendicular bisectors of the sides of the triangle intersect.

Label the vertices of the triangle:

• A = (-6, 5)
• B = (-3, -4)
• C = (2, 1)

We only need to find the perpendicular bisectors of two of the sides.

To find the perpendicular bisectors, first find the slope of the two lines by using the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

The slope of AB is:

`m_(AB)=(y_B-y_A)/(x_B-x_A)=(-4-5)/(-3-(-6))=(-9)/(3)=-3`

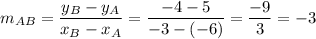
Therefore, the slope of the perpendicular bisector of AB is 1/3.

The slope of AC is:

`m_(AC)=(y_C-y_A)/(x_C-x_A)=(1-5)/(2-(-6))=(-4)/(8)=-(1)/(2)`

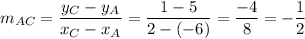
Therefore, the slope of the perpendicular bisector of AC is 2.

Now find the midpoints of two of the line segments by using the midpoint formula:

`(x_m,y_m)=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

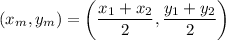
The midpoint of AB is:

`\implies \left((x_A+x_B)/(2),(y_A+y_B)/(2)\right)=\left((-6+(-3))/(2),(5+(-4))/(2)\right)=\left(-(9)/(2),(1)/(2)\right)`

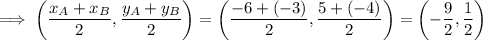
The midpoint of AC is:

`\implies \left((x_A+x_C)/(2),(y_A+y_C)/(2)\right)=\left((-6+2)/(2),(5+1)/(2)\right)=\left(-2,3\right)`

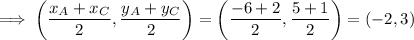
Now we can create equations for the perpendicular bisectors of AB and AC by substituting the found slopes and midpoints into the point-slope formula:

`y-y_1=m(x-x_1)`

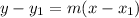
The equation of the perpendicular bisector of AB is:

`\implies y-(1)/(2)=(1)/(3)\left(x-\left(-(9)/(2)\right)\right)`

`\implies y-(1)/(2)=(1)/(3)x+(3)/(2)`

`\implies y=(1)/(3)x+2`

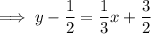
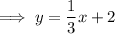
The equation of the perpendicular bisector of AC is:

`\implies y-3=2\left(x-\left(-2\right)\right)`

`\implies y-3=2x+4`

`\implies y=2x+7`

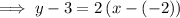
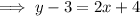
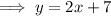
Now we have equations for the perpendicular bisectors of two of the sides of the triangle, we can find the x-value of the point of intersection (the circumcenter) by equating the equations and solving for x:

`\implies 2x+7=(1)/(3)x+2`

`\implies (5)/(3)x=-5`

`\implies x=-3`

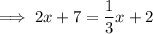
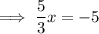
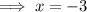
Substitute the found value of x into one of the equations and solve for y:

`\implies y=2(-3)+7=1`

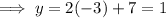
Therefore, the coordinates of the point equidistant from the position of the three students is (-3, 1).

To find the equation of the locus of the circular path, we need to find the equation of the circle with center at (-3, 1) and radius equal to the distance from any of the three students to the center.

To find the radius of the circle, calculate the distance between the center (-3, 1) and one of the points using the distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Therefore, the distance between the center (-3, 1) and point A (-6, 5) is:

`\implies r=√((-6-(-3))^2+(5-1)^2)`

`\implies r=√((-3)^2+(4)^2)`

`\implies r=√(25)`

`\implies r=5`

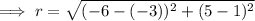
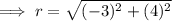
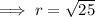
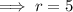
Finally, substitute the found center and radius into the general equation of a circle:

`(x-h)^2+(y-k)^2=r^2`

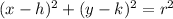
where (h, k) is the center, and r is the radius.

Therefore, the equation of the circle is:

`(x+3)^2+(y-1)^2=25`

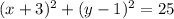
Expanding to give the equation of the locus of the circular path:

`\implies x^2+6x+9+y^2-2y+1=25`

`\implies x^2+y^2+6x-2y-15=0`