Question

A parabola opening up or down has vertex (0, 0) and passes through (-4, -2). Write its

equation in vertex form.
Simplify any fractions.

Answer 1

Answer: y =
`(-(1)/(8)) x^2`

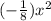
Explanation:

Since the vertex is at (0,0), the vertex form of the equation of the parabola is y = a(x - 0)^2 + 0 or simply y = ax^2.

To find the value of a, we can use the point (-4, -2) that the parabola passes through:

-2 = a(-4)^2

-2 = 16a

a = -1/8

Therefore, the equation of the parabola in vertex form is y = (-1/8)x^2.