Question

Identify the polynomial that is the difference of two squares.

25m^2 − 16n
9m^2 − 5n^6
49m^2 − 81n^4
36m^2 − 8n^8

Answer 1

`25m² − 16n`

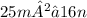
Explanation:

The polynomial that is the difference of two squares is:

`25m^2 − 16n`

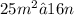
To see why, we can try to factor each polynomial. For example:

`9m^2 − 5n^6 = (3m)^2 − (n^3)^2`

`49m^2 − 81n^4 = (7m)^2 − (9n^2)^2`

`36m^2 − 8n^8 = (6m)^2 − (2n^4)^2`

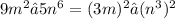
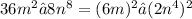
Notice that for each of these polynomials, we can factor them into the difference of two squares. However, for the polynomial 25m² − 16n, we can directly see that it is the difference of two squares because:

`25m^2 − 16n = (5m)^2 − (4n)^2`

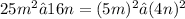
Therefore, 25m² − 16n is the polynomial that is the difference of two squares.