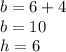Question

The base of triangle exceeds the height by 4cm if the area is 30cm² then find the langth of base & hight of triangle​

Answer 1

Base = 10 cm

Height = 6 cm

Explanation:

Here is the formula for the area of a triangle.

`A=(bh)/(2)`

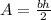
We are given

`A=30`

`b=h+4`

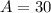
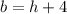
Replace all occurrences of
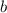`b` with
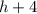`h+4` in each equation.

`(h+4)*(h)/(2) =30`

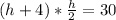
Apply the distributive property.

`h((h)/(2))+4((h)/(2))=30`

`(h*h)/(2)+4((h)/(2))=30`

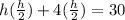
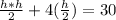
Use the power rule to combine exponents.

`(h^2)/(2)+4((h)/(2))=30`

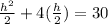
Factor 2 out of 4 .

`(h^2)/(2)+2(2)((h)/(2))=30`

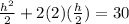
Cancel the common factor.

`(h^2)/(2)+2h=30`

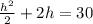
Solve for h.

Multiply each term in
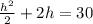`(h^2)/(2)+2h=30` by 2 to eliminate the fractions.

`(h^2)/(2)*2+2h*2=30*2`

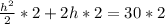
Simplify each term.

Cancel the common factor of 2.

`h^2+2h*2=30*2`

`h^2+4h=60`

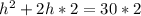
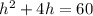
Subtract 60 from both sides of the equation.

`h^2+4h-60=0`

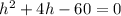
Factor using the AC method.

Consider the form
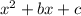`x^2+bx+c` . Find a pair of integers whose product is
`c` and whose sum is
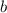`b` . In this case, whose product is − 60 and whose sum is 4 .

−6, 10

Write the factored form using these integers.

`(h-6)(h+10)=0`

Set
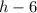`h-6` equal to 0 and solve for h.

Then add 6 to both sides of the equation.

`h-6=0\\h=6`

Set
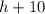`h+10` equal to 0 and solve for h.

Then subtract 10 from both sides of the equation.

`h+10=0\\h=-10`

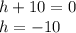
The final solution is all the values that make
`(h-6)(h+10)=0` true.

`h=6,-10`

Given
`b=h+4`

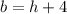
Replace all occurrences of h with 6 in each equation.

`b=6+4\\b=10\\h=6`