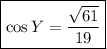Question

Express cos Y as a fraction in simplest terms.

Answer 1

`\Large\boxed{\sf \cos Y =(√(61))/(19)}`

Explanation:

We are interested in expression cosY in simplest terms. In any right angled triangle, cosine is defined as the ratio of base and hypotenuse. The side opposite to the right angle or the longest side of the triangle is hypotenuse. From the given triangle, we can see that;

• base = √61
• Hypotenuse = 19 .

So we may find cosY as ,

`\implies \cos\theta =(b)/(h) \\`

substitute the respective values,

`\implies \cos\theta =(√(61))/(19) \\`

Here the angle is Y , so that ;

`\implies \underline{\underline{\red{ \cos\rm{Y}=(√(61))/(19)}}} \\`

This is the required answer in simplest form as the HCF of √61 and 19 is 1 .

Answer 2

`\cos Y=(√(61))/(19)`

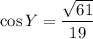
Explanation:

To find the cosine of an angle in a right triangle, use the cosine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Cos trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

From inspection of the given right triangle WXY, the side adjacent to angle Y is XY, and the hypotenuse is WY. Therefore:

• θ = Y
• A = XY = √(61)
• H = WY = 19

Substitute these values into the formula:

`\implies \cos Y=(√(61))/(19)`

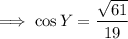
As 61 and 19 are prime numbers, the fraction cannot be simplified further.

Therefore, cos Y expressed as a fraction in simplest terms is:

`\boxed{\cos Y=(√(61))/(19)}`