Question

Please help me I can figure it out

Answer 1

(2x -4)/(x -1)

Explanation:

You want to simplify (2x² -2x -4)/(x² -1).

Factors

Simplifying a rational expression generally means cancelling common factors from the numerator and denominator. To do that, you must factor both the numerator and the denominator.

Numerator

The numerator coefficients have a common factor of 2. Removing that can simplify the problem of factoring the numerator:

2x² -2x -4 = 2(x² -x -2)

To factor the quadratic, you look for factors of -2 that have a sum of -1. Those would be -2 and +1. The middle term is written as a sum using these values.

= 2(x² -2x +x -2)

This can now be factored by grouping terms in pairs, and factoring each pair.

= 2((x² -2x) +(x -2)) = 2(x(x -2) +1(x -2))

= 2(x +1)(x -2)

Denominator

The denominator is the difference of squares, so is factored according to the pattern for that:

a² -b² = (a -b)(a +b)

x² -1 = (x -1)(x +1)

Simplified form

Now you know enough to be able to simplify the expression. The common factors (x+1) cancel.

`(2x^2-2x-4)/(x^2-1)=(2(x+1)(x-2))/((x+1)(x-1))\\\\=(2(x-2))/(x-1)=\boxed{(2x-4)/(x-1)}`

__

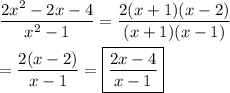
Additional comment

Even though the factor (x+1) has disappeared from the expression, the simplified form still carries the restriction that x ≠ -1. The graph of the original expression will have a "hole" at (-1, 3), where it is undefined. Otherwise, the graph looks like a graph of (2x-4)/(x-1).