Question

Use the Law of Cosines to solve the problem. You must solve for BC first. Solve this order

A ship travels due west for 94 miles. It then travels in a northwest direction for 119 miles and ends up 173 miles from its original position. To the nearest tenth of a degree, how many degrees north of west (x) did it turn when it changed direction? Show you Work.

Answer 1

answer: 175

Explanation:

Answer 2

71.9 degrees

Explanation:

The find the value of x on the given diagram, we must first find the included angle between the two line segments labelled 94 mi and 119 mi in the triangle. To do this, we can use the Law of Cosines.

`\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

The values to substitute into the formula are:

• a = 119
• b = 94
• c = 173

Solving for the angle C:

`\begin{aligned}173^2&=119^2+94^2-2(119)(94)\cos C\\\\29929&=14161+8836-22372\cos C\\\\29929&=22997-22372\cos C\\\\6932&=-22372\cos C\\\\-(6932)/(22372)&=\cos C\\\\C&=\cos^(-1)\left(-(6932)/(22372)\right)\\\\C&=108.0502874...^(\circ)\end{aligned}`

As angles on a straight line sum to 180°, the value of x can be calculated by subtracting the found value of C from 180°:

`x=180^(\circ)-108.0502874...^(\circ)`

`x=71.9497125...^(\circ)`

`x=71.9^(\circ)\; \sf (nearest\;tenth)`

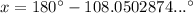
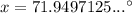
Therefore, the ship turned 71.9 degrees north of west when it changed direction.