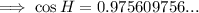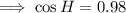Question

Find the value of cos H rounded to the nearest hundredth, if necessary.

Answer 1

Given:-

• A right angled triangle right angled at I is given to us.
• The measure of the longest side (hypotenuse) is 41 and the other two sides are 40 and 9 .

To find:-

• The value of cosH .

Answer:-

In the given right angled triangle, cosine is the ratio of base and hypotenuse. In this triangle with respect to angle H , IH is base, IJ is perpendicular and JH is hypotenuse. And their measures are ,

• HJ = 41
• IH = 40
• IJ = 9 .

And as mentioned earlier, we can find cosH as ,

`\implies\cos\theta =(b)/(h) \\`

`\implies \cos H =(IH)/(HJ) \\`

On substituting the respective values, we have;

`\implies\cos H = (40)/(41)\\`

`\implies \cos H = 0.975`

Value rounded to nearest hundred will be ,

`\implies \cos H =\boxed{0.98}`

Hence the value of cos H 0.98 .

Answer 2

cos H = 0.98 (rounded to the nearest hundredth)

Explanation:

Answer:

`\cos R=(3)/(5)`

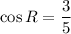
Explanation:

To find the cosine of an angle in a right triangle, we can use the cosine trigonometric ratio.

The cosine trigonometric ratio is the ratio of the side adjacent to the angle to the hypotenuse.

`\boxed{\cos \theta=\sf (A)/(H)}`

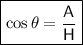
From inspection of the given right triangle HIJ, the side adjacent to angle H is IH, and the hypotenuse is HJ. Therefore:

• θ = H
• A = IH = 40
• H = HJ = 41

Substitute these values into the formula:

`\implies \cos H=(40)/(41)`

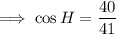
As 41 is a prime number, the fraction cannot be reduced any further.

The value of cos H rounded to the nearest hundredth is:

`\implies \cos H=0.975609756...`

`\implies \cos H=0.98`