Im being timed which number line represents the solution set for the inequality?

Question

asked Jul 10, 2022 53.2k views

1 Answer

Noble Polygon · Answer 1 · 2022-07-16T01:04:00+0000

Answer:

The solution is:

$-(1)/(2)x\ge \:4\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\le \:-8\:\\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-8]\end{bmatrix}$

The number line graph of the solution is also attached below.

From the graph, it is clear that the 2nd number line represents the solution set for the inequality.

Explanation:

Given the inequality

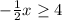
$-(1)/(2)x\ge 4$

Let us solve the inequality

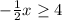
$-(1)/(2)x\ge 4$

Multiply both sides by -1 (reverse the inequality)

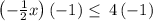
$\left(-(1)/(2)x\right)\left(-1\right)\le \:4\left(-1\right)$

Simplify

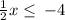
$(1)/(2)x\le \:-4$

Multiply both sides by 2

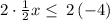
$2\cdot (1)/(2)x\le \:2\left(-4\right)$

Simplify

$x\le \:-8$

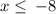
Thus, the solution is:

$-(1)/(2)x\ge \:4\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\le \:-8\:\\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-8]\end{bmatrix}$

The number line graph of the solution is also attached below.

From the graph, it is clear that the 2nd number line represents the solution set for the inequality.