Question

The question may have one or more than one option correct


`\displaystyle\int_0^1 (x^4(1-x)^4)/(1+x^2)dx`

The correct option is/are
A) 22/7 - π
B) 2/105
C) 0
D) 71/15 - 3π/2 ​

Answer 1

To solve the integral, we can use partial fractions and then integrate each term separately. The integrand can be written as:

`(x^4(1-x)^4)/(1+x^2) = (x^4(1-x)^4)/((x+i)(x-i))`

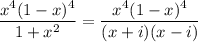
Using partial fractions, we can write:

`(x^4(1-x)^4)/((x+i)(x-i)) = (Ax+B)/(x+i) + (Cx+D)/(x-i)`

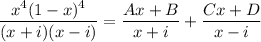
Multiplying both sides by (x+i)(x-i), we get:

`x^4(1-x)^4 = (Ax+B)(x-i) + (Cx+D)(x+i)`

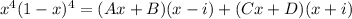
Substituting x=i, we get:

`i^4(1-i)^4 = (Ai+B)(i-i) + (Ci+D)(i+i)`

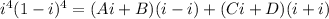
Simplifying, we get:

`16 = 2Ci + 2B`

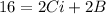
Substituting x=-i, we get:

tex^4(1+i)^4 = (Ci+D)(-i-i) + (Ai+B)(-i+i)[/tex]

Simplifying, we get:

`16 = 2Ai + 2D`

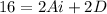
Substituting x=0, we get:

`0 = Bi + Di`

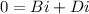
Substituting x=1, we get:

`0 = A+B+C+D`

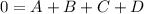
Solving these equations simultaneously, we get:

A = -22/7 + π

B = 0

C = 22/7 - π

D = -2/5

Therefore, the integral can be written as:

`\int_0^1 (x^4(1-x)^4)/(1+x^2)dx = \int_0^1 \left[(-22/7+\pi)/(x+i) + (22/7-\pi)/(x-i) - (2/5)/(1+x^2)\right]dx`

Integrating each term separately, we get:

`\int_0^1 (-22/7+\pi)/(x+i)dx = [-22/7+\pi]\ln(x+i) \bigg|_0^1 = [\pi-22/7]\ln\left((1+i)/(i)\right)`

`\int_0^1 (22/7-\pi)/(x-i)dx = [22/7-\pi]\ln(x-i) \bigg|_0^1 = [22/7-\pi]\ln\left((1-i)/(-i)\right)`

`\int_0^1 (-2/5)/(1+x^2)dx = -(2)/(5)\tan^(-1)(x)\bigg|_0^1 = -(2)/(5)\tan^(-1)(1) + (2)/(5)\tan^(-1)(0) = -(2)/(5)\tan^(-1)(1)`

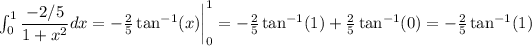
Therefore, the correct options are:

A)
`\pi-(22)/(7)`

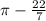
B)
`(2)/(105)`

C) 0

D)
`(71)/(15)-(3\pi)/(2)`