Question

Find any critical numbers of the function.

Answer 1

(1, 2) and (-1, -2). or. (±1, ±2)

Explanation:

`{ \sf{f(x) = \frac{4x}{ {x}^(2) + 1 } }} \\`

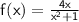
- Simply, a critical number or critical point is gotten by differentiating the function.

From Quotient rule;

`{ \sf{ {f}^(l)(x) = \frac{4( {x}^(2) + 1) - (2x)(4x)}{ {( {x}^(2) + 1)}^(2) } }} \\ \\ { \sf{f {}^(l)(x) = \frac{ {4x}^(2) + 4 - {8x}^(2) }{ {( {x}^(2) + 1) }^(2) } }} \\ \\ { \sf{f {}^(l)(x) = \frac{4(1 - {x}^(2)) }{ {( {x}^(2 ) + 1) }^(2) } }}`

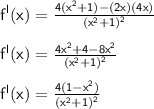
Then equate this derivative to zero;

`{ \sf{0 = \frac{4(1 - {x}^(2) )}{ {( {x}^(2) + 1) }^(2) } }} \\ \\ { \sf{4(1 - {x}^(2) ) = 0}} \\ \\ { \sf{4 - {4x}^(2) = 0}} \\ \\ { \sf{4 {x}^(2) = 4}} \\ \\ { \sf{x = √(1) }} \\ \\ { \sf{ \underline{ \: x = \pm 1 \: }}}`

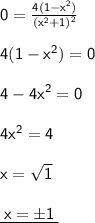
Substitute for x in f(x)

For x = 1

`{ \sf{f(1) = \frac{4(1)}{ {(1)}^(2) + 1} = (4)/(2) = 2 }} \\`

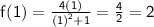
For x = -1

`{ \sf{f( - 1) = \frac{4( - 1)}{ {( - 1)}^(2) + 1 } = ( - 4)/(2) = - 2 }} \\`

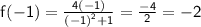
Therefore points are;

(1, 2) and (-1, -2)