Question

Find two numbers whose sum is 28 and whose product is the maximum possible value. What two numbers yield this product?

Answer 1

`the \: two \: numbers \: are \: 14 \: and \: 14.`

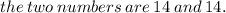
Explanation:

let x, y be the two numbers

:

x + y = 28

:

if the two numbers are 1 and 27, then

:

1) x + y = 28

:

2) xy = 27

:

solve equation 1 for y, then substitute for y in equation 2

:

3) y = 28 -x

:

x(28-x) = 27

:

4) -x^2 +28x -27 = 0

:

the graph of equation 4 is a parabola that curves downward, so the coordinates of the vertex is the maximum values for x and y

:

x coordinate = -b/2a = -28/2(-1) = 14

:

substitute for x in equation 3

:

y = 28 -14 = 14

:

*****************************************************

the maximum product occurs when x=14 and y=14

:

Note 14 * 14 = 196