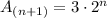Question

Image attached, please help.

Answer 1

Explanation:

so, it is a geometric sequence (every new term is created by multiplying the previous term by a fixed constant.

in this case this constant is 2.

a1 = 3

a2 = 3×2 = 6

a3 = a2×2 = a1 × 2×2 = 3×4 = 12

so, we see

an = 3 ×2^(n-1)

or

an+1 = 3 × 2^n

Answer 2

`A_n=3 \cdot 2^(n-1)`

Explanation:

A recursive formula for a sequence allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.

Given recursive rule:

`\begin{cases}A_1=3\\A_((n+1))=2A_n\end{cases}`

According to the recursive formula, each term in the sequence is double the previous term. This means the sequence is geometric with the common ratio, r = 2.

An explicit formula for a sequence allows you to find the nth term of the sequence. The explicit formula for a geometric sequence is:

`\boxed{A_n=A_1 \cdot r^(n-1)}`

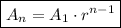
where:

• A₁ is the first term.
• r is the common ratio.

Substituting the given value of A₁ and the found value of r into the formula, the explicit formula for the given sequence is:

`A_n=3 \cdot 2^(n-1)`

This can also be written as:

`A_((n+1))=3 \cdot 2^(n)`